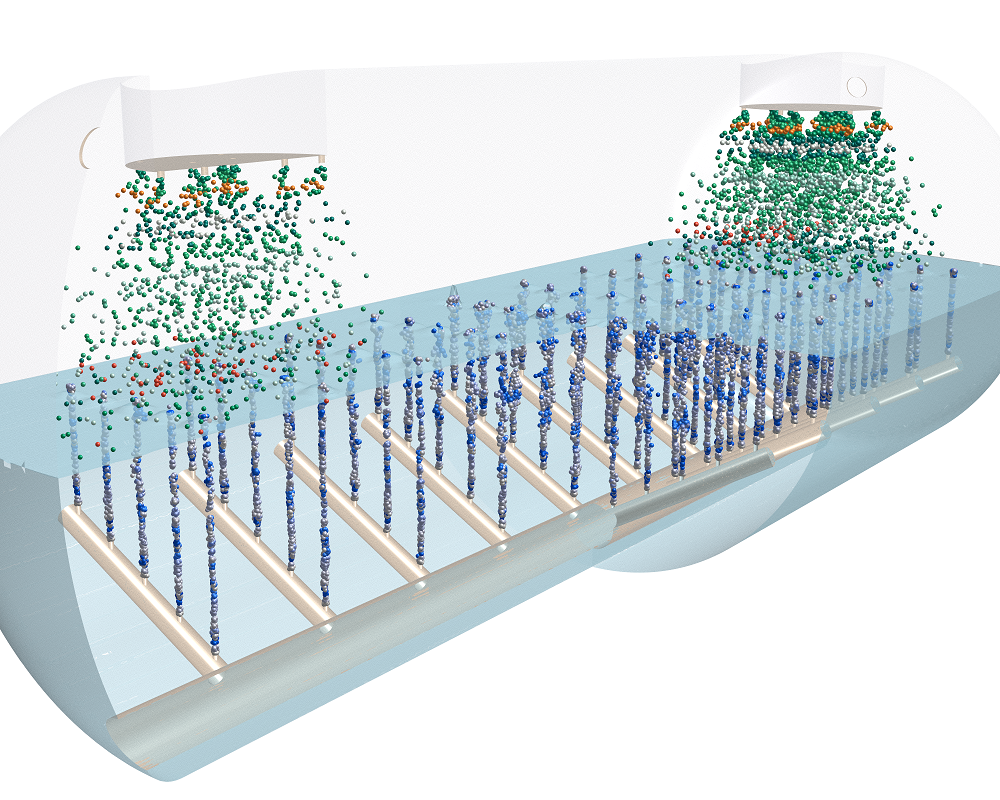
Generally speaking, there are two classes of multiphase flow: dispersed flows and separated flows. In order to make accurate predictions, an engineer must be knowledgeable in both the physical nature and the numerical modeling approaches specific to each.

In dispersed flows, a secondary phase is distributed at low volume fractions within a primary, continuous phase. The canonical example is that of gaseous bubbles in a liquid. In separated flows, two or more continuous streams of different fluids are separated by interfaces where. The canonical example is a hydrological flow where there is a clearly visible boundary separating the heavier water from air.

For separated flows, the recently introduced Volume of Fluid (VOF) method allows us to accurately track the motion of the interfaces between phases and model phase change effects like boiling, evaporation, condensation, cavitation, solidification and melting. This model is well suited for applications including marine hydrodynamics and seakeeping, river and dam hydraulics, stormwater runoff and drains, and wastewater treatment plants.

For dispersed multiphase simulations we typically lean on two core modeling approaches. The first, called the Eulerian method, comes in two flavors. The simpler of the two, the multiphase mixture model, assumes a single phase that acts as a mass weighted combination of the two phases at all locations. The second, more complicated method, models each of the phases in its full Navier-Stokes glory with phase interactions defined by slip velocity and other empirically derived relations. These Eulerian method are commonly used in modeling fluidized beds, miscible and immiscible mixtures, and bubbly flows.

The second approach, known as the Lagrangian method, models the continuous phase according to the Navier-Stokes equations but the secondary, dispersed phase as a collection of discrete parcels, each obeying Newton’s laws of motion. Each of these phases can impact the other through any number of physical interaction mechanisms according to the user’s discretion.

All of the multiphase models discussed here can be combined in any fashion with one another and with other physics models such as chemical reactions, turbulence models, conjugate heat transfer, radiation, and electrodynamics.