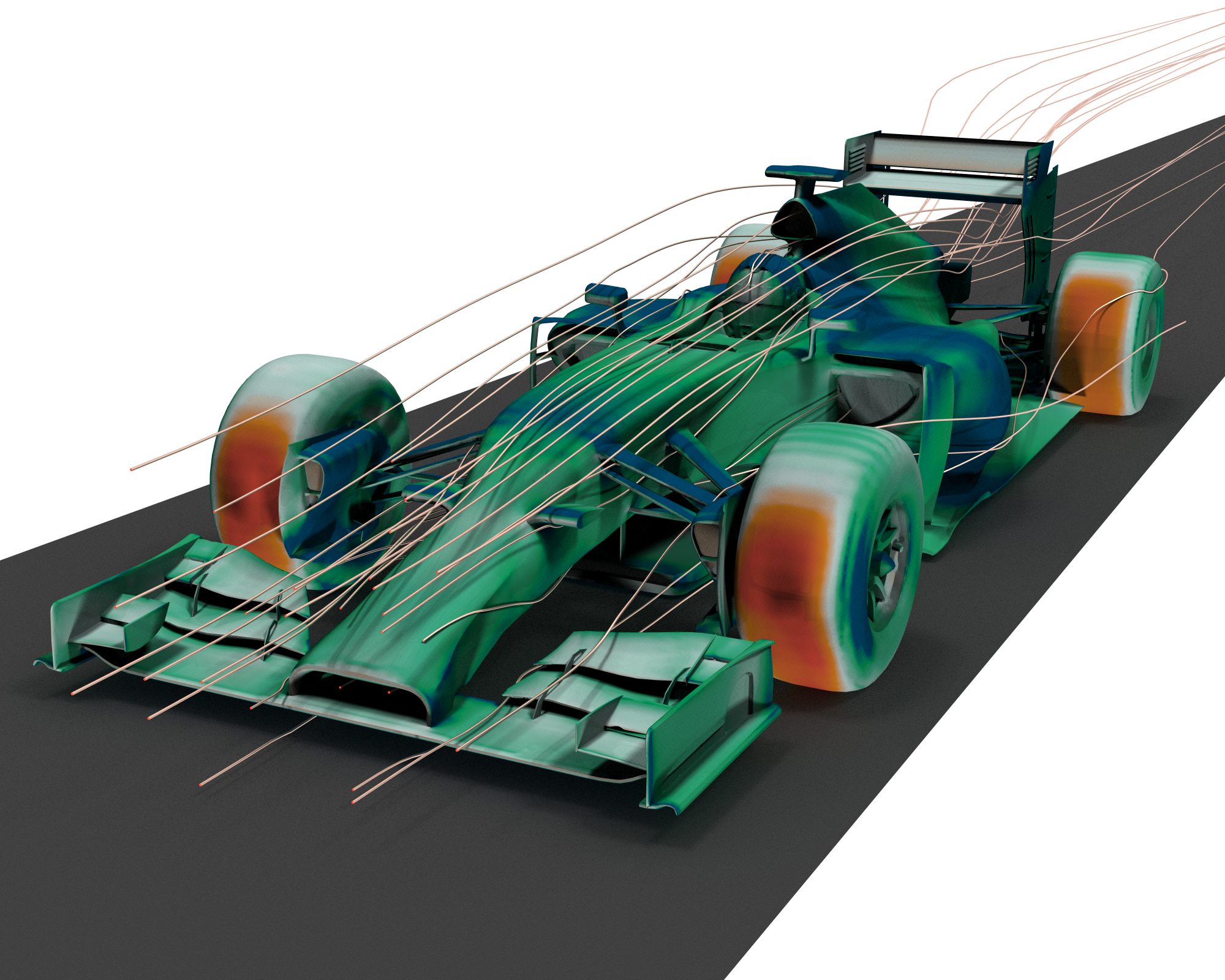
An Introduction to CFD Mesh Quality

Does Mesh Quality Impact the Accuracy of CFD Simulations

In the field of Computational Fluid Dynamics (CFD), accurate predictions are crucial for engineers, researchers, and designers alike. One critical factor that significantly affects the accuracy of CFD simulations is the quality of the mesh used in the analysis. A mesh is a discretized representation of the computational domain, consisting of nodes and elements that define the shape and connectivity of the problem. In this article, we delve into the topic of mesh quality and explore its impact on the accuracy of CFD simulations.

Visual and Quantitative Inspection of Mesh Quality

Before analyzing the influence of mesh quality on CFD simulations, it is essential to understand how to assess the quality of a given mesh. Visual inspection provides a quick overview of the mesh's characteristics, including element shape, skewness, and smoothness near boundaries or areas of interest. However, visual inspection alone may not provide a comprehensive evaluation.

When visually inspecting a mesh, it is important to consider various factors. One aspect to look for is the overall element shape. Ideally, elements should be as close to regular shapes, such as triangles or quadrilaterals, as possible. Irregularly shaped elements can lead to inaccuracies in the simulation results. Additionally, the skewness of elements should be examined. Skewness refers to the angular deformation of an element, and high skewness values can indicate poor mesh quality.

Another aspect to consider during visual inspection is the smoothness of the mesh near boundaries or areas of interest. Smoothness refers to the absence of abrupt changes or irregularities in the mesh. A smooth mesh ensures that the flow of fluid or air through the simulation domain is not hindered by discontinuities in the mesh.

While visual inspection provides valuable insights into the mesh quality, it is often necessary to complement it with quantitative measures. These measures offer a more detailed examination of the mesh quality, allowing for a more comprehensive evaluation.

One commonly used quantitative measure is the aspect ratio. The aspect ratio quantifies the elongation or distortion of elements. A high aspect ratio indicates that the elements are highly elongated or distorted, which can negatively impact the accuracy of the simulation. On the other hand, a low aspect ratio suggests that the elements are closer to regular shapes, leading to more reliable results.

Skewness is another important quantitative measure. It assesses the angular deformation of elements. High skewness values indicate that the elements are significantly deformed, which can introduce errors in the simulation. Low skewness values, on the other hand, indicate that the elements are closer to being regular, ensuring more accurate results.

In addition to aspect ratio and skewness, orthogonality is another quantitative measure used to evaluate mesh quality. Orthogonality measures the deviation from perpendicularity between adjacent elements. A high orthogonality value indicates that the elements are nearly perpendicular to each other, which is desirable for accurate simulations. Conversely, a low orthogonality value suggests that the elements are significantly deviated from perpendicularity, potentially leading to inaccuracies.

Cell volume is yet another quantitative measure that aids in assessing mesh quality. It helps identify distorted or collapsed elements by measuring the volume of each cell in the mesh. A significant deviation from the expected cell volume can indicate mesh irregularities that may affect the simulation results.

By combining visual and quantitative inspection, engineers and researchers can obtain a thorough characterization of mesh quality. Visual inspection provides a quick overview, while quantitative measures offer detailed insights into specific aspects of the mesh. This comprehensive evaluation allows for the identification of potential issues and the improvement of mesh quality, ultimately leading to more accurate and reliable CFD simulations.

Stability and Convergence

Mesh quality has a direct impact on the stability and convergence of CFD simulations. A high-quality mesh with well-shaped elements ensures numerical stability and efficient convergence of the governing equations. On the other hand, a low-quality mesh can lead to non-physical results, instability, and numerical divergence.

Stability refers to the ability of a numerical method to produce consistent and reliable results. A poor-quality mesh can introduce numerical errors and instability, compromising the stability of the simulation. Such instability manifests in oscillations, unphysical behavior, or even the failure of the numerical solver to converge.

Convergence is another critical aspect affected by mesh quality. A convergence study evaluates the rate at which the numerical solution approaches the exact solution as the mesh is refined. A well-converged solution exhibits minimal changes with increasing mesh density. In contrast, a poorly converged solution indicates the need for improved mesh quality to obtain accurate results.

Let's delve deeper into the concept of stability in CFD simulations. Stability is crucial because it ensures that the numerical solution remains bounded and does not exhibit wild fluctuations. When a simulation is unstable, it becomes challenging to trust the results obtained. The accuracy and reliability of the simulation are compromised, making it difficult to draw meaningful conclusions.

One common manifestation of instability in CFD simulations is the presence of oscillations. These oscillations can occur in the flow variables, such as velocity or pressure, and can lead to unphysical behavior. For example, in a simulation of fluid flow around an airfoil, an unstable solution may result in the airfoil experiencing sudden and unrealistic fluctuations in lift or drag forces.

In addition to oscillations, instability can also cause the numerical solver to fail to converge. Convergence refers to the process by which the numerical solution approaches the exact solution as the computational grid is refined. When a simulation fails to converge, it means that the solution is not getting closer to the true solution, even with increasing computational effort.

Now, let's shift our focus to the concept of convergence in CFD simulations. Convergence is a measure of how well the numerical solution approximates the exact solution. It is essential to ensure that the numerical solution is independent of the grid resolution, meaning that refining the mesh should not significantly alter the results.

A well-converged solution exhibits minimal changes as the mesh is refined. This means that the solution is approaching the exact solution, and further mesh refinement will not significantly affect the results. On the other hand, a poorly converged solution indicates that the numerical solution is highly dependent on the mesh quality.

Improving mesh quality is crucial to obtaining accurate and reliable results. Mesh quality can be improved by ensuring that the elements are well-shaped and have suitable aspect ratios. Well-shaped elements reduce numerical errors and improve the stability and convergence of the simulation.

In conclusion, stability and convergence are essential considerations in CFD simulations. A high-quality mesh with well-shaped elements is crucial for ensuring numerical stability and efficient convergence. Unstable simulations can lead to non-physical results, oscillations, and failure to converge. Convergence studies help evaluate the accuracy of the numerical solution, and a well-converged solution exhibits minimal changes with increasing mesh density. Improving mesh quality is vital to obtaining accurate and reliable results in CFD simulations.

CFL Number and y+

The choice of mesh quality relates to specific parameters used in CFD simulations, such as the CFL number and y+. The CFL number, or Courant-Friedrichs-Lewy number, characterizes the time-step size in relation to the grid spacing. For stable and accurate simulations, the CFL number should be constrained within certain limits, which, in turn, depend on the mesh quality.

The parameter y+, known as the dimensionless wall distance or wall proximity, determines the resolution of the near-wall region. A proper y+ value ensures an accurate representation of the boundary layer physics. Achieving an appropriate y+ depends on both the wall function used and the mesh quality, specifically the near-wall element sizing.

Grid Convergence Testing

Grid convergence testing is a systematic approach to assess the impact of mesh quality on CFD simulations. It involves refining the mesh and comparing simulation results against a reference solution obtained from a more refined mesh. By progressively refining the mesh until the results show minimal changes, engineers can determine the mesh size at which convergence is achieved.

Grid convergence testing provides valuable insights into the sensitivity of the results to the mesh quality. It helps identify regions where the mesh should be improved to enhance accuracy and reduce uncertainties. Additionally, it serves as a validation method for the simulation setup, ensuring that the results are mesh-independent and reliable.

Conclusion

In conclusion, the quality of the mesh significantly impacts the accuracy of CFD simulations. Visual and quantitative inspection techniques are essential for evaluating mesh quality. Through stable and converged simulations, the influence of mesh quality can be observed on parameters like the CFL number and y+. Grid convergence testing aids in determining the optimal mesh size for accurate predictions. By understanding the impact of mesh quality, engineers and researchers can enhance the reliability and credibility of CFD simulations in various fields.